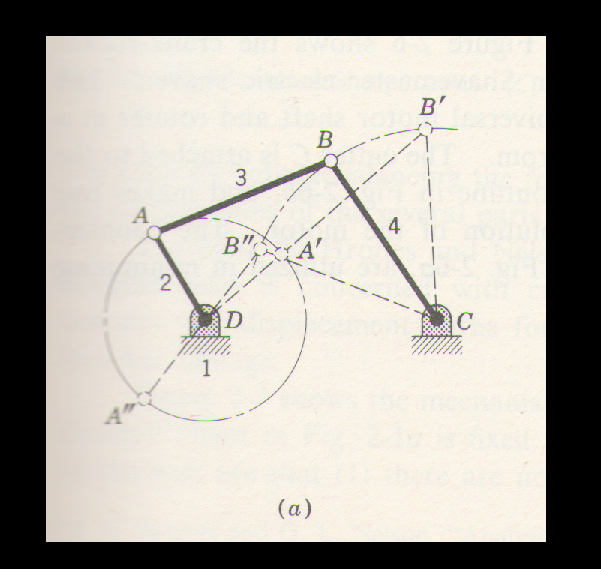
Let us take the case of the Grashof Linkage where the sum of the lengths of the shortest and the longest Link is less than the sum of the length of the other two sides.
In the Fig., posted above, The limiting phases of the four-bar Grashof linkage are shown. In these cases the fourth link has been formed, as can be seen, by fixing one to the links adjacent to the shortest link. Refer to Fig. (a) the sum of the shortest and the longest links is less than the sum of the other two sides.
The formation of the linkage in Fig.(b) is similar to that of Fig.(a) except that the length of the linkage CD has been increased.
In Fig.(b). you can see that the sum of the length of the shortest and the longest links is equal to the sum of the lengths of the other two sides.
Both the linkages, mentioned above, have drivers (link 2) that rotates to make the follower link(4) oscillate, as such both fall in the category of Crank-rocker mechanisms, but there is some difference between the two.
The mechanism of Fig.(a) has a driver 'without' a dead-centre-phase (look at the position of joint at position A') whereas, in Fib.(b) we have a dead-centre-phase with A and B in simultaneous dead-centre-positions at A" and B" respectively.
The important point to note, therefore, is that at the simultaneous dead-centre-positions for links 2 and 4 are not totally constrained. It means that they are capable of rotating either way. Because of this the direction of rotation can change at A" and B". These points are, therefore, called change points.

No comments:
Post a Comment